MENU
  1. ホーム
  2. ノート
  3. lect
  4. GAMESSではじめる量子化学計算

GAMESSではじめる量子化学計算

lect

このコンテンツとほぼ全く同じ内容を「YamLab オンラインコース」にも掲載しています。教材として使いやすい方をご利用ください。

目次

この講座について

  • GAMESS とは、量子化学の知識や技術に基づいて分子の様々な性質を解析しようとするときに使う量子化学計算用のプログラムです。
  • GAMESS の魅力として挙げられるのは、まずは、無償で利用できること。そして、量子化学計算のメジャーな手法だけではなく、他のプログラムでは実装されていないマイナー（と言うとその手法の開発者に怒られそうだけれど）な手法も利用できること。
  • この講座では、計算化学の研究室に配属になったばかりの学生に読んでもらうようなことを考えながら、GAMESS の基本的な使い方、そして、量子化学計算に取り組むときに知っておくと助けになることについて、ざっくりとご紹介します。

量子化学計算とは？

量子化学計算で何ができる？

量子化学計算は、物質の様々な性質を特徴付けている微視的な物性諸量を知りたいと思うときに、解析や予測の助けとなる便利な道具です。

機能性材料 を設計しようとしたり、新しい薬 を開発しようとするときに、研究・開発の現場では様々な課題に直面することもあります。そのようなときに量子化学計算は、対象としている物質の分子レベルでのふるまいを明らかにすることで、問題を解決するための様々な手がかりを与えてくれます。

たとえば、量子化学計算を活用すると、物質を構成している分子の形、安定性、分子同士の相互作用の強さ、化学反応の起こりやすさなどについて、ある程度の定量的な精度で信頼できる予測を理論的に導きだすことができます。

業界標準は Gaussian

量子化学計算を利用できるプログラムは数多くあるのですが、デファクトスタンダード（事実上の業界標準） は商用パッケージである Gaussian であると言えます。GaussView というアプリと併せて使うと、マウスでボタンをポチッとするだけで、高機能な量子化学計算をお手軽に実行できることは大きな魅力です。

また、コンピュータを使って分子のことを調べている私のような計算化学者だけではなく、化合物を合成したり装置を使って分析している実験化学者にも Gaussian ユーザーがたくさんいます。もし分からないことがあったり、困ったことがあったときにも、適切なアドバイスをしてくれるひとがすぐに見つかることが多いですし、インターネットの検索で有益な情報をたくさん得ることができたりします。

無料で使える GAMESS

今回紹介する GAMESS は、有名な商用パッケージである Gaussian に次ぐ規模での利用実績があって、高度な機能を備えていながら、無償で配布されています。またこの GAMESS は、量子化学計算について基本的なことがひととおりできるというだけではなく、最先端で開発が進められている様々な新しい手法を実行できること、そして、公開されているソースコードに基づいてオリジナルの機能をこのパッケージに追加することができることも、大きな魅力だと思っています。

オススメの参考書

GAMESS に興味がある方には、このノートを読んでざっくりと使ってみた後に、次のような、その使い方などが丁寧に・詳しく解説されている優れた解説書（1, 2） 、量子化学の入門書 (3) 、教科書 (4) などを読んで、時間をかけてじっくりと勉強してみることもオススメします。

ゼロからわかる!! 独習 量子化学計算: 理論からはじめない新しい量子化学計算の本
著:久我 涼子
¥3,284 （2024/04/13 22:01時点 | Amazon調べ）
Amazon
量子化学計算ソフト GAMESSとFireflyの使い方 -解説と入力ファイル付きマニュアルー
著:毛利 文仁
¥3,850 （2024/04/13 22:01時点 | Amazon調べ）
Amazon
はじめての量子化学 量子力学が解き明かす化学の仕組み (ブルーバックス)
講談社
¥1,320 （2024/04/13 22:02時点 | Amazon調べ）
Amazon
量子化学 下巻
著:原田 義也
¥5,720 （2024/04/13 22:03時点 | Amazon調べ）
Amazon

GAMESSの概要

オリジナル版 GAMESS

GAMESS は、分子の電子状態を解析するための量子化学計算プログラムです。この少し変わった名前は、General Atomic and Molecular Electronic Structure System の頭文字だと言われています。

GAMESS には、現在、アメリカ版（GAMESS-US）、イギリス版（GAMESS-UK）、そして、Firefly という３つの異なるバージョンがあります。

どのバージョンも、1970年代後半にアメリカ・エネルギー省の NRCC（National Resource for Computational Chemistry）というプロジェクトで開発されたプログラムコードが共通の先祖のようです。

オリジナル版 GAMESS は、1981年にまずはアメリカ版（GAMESS-US）とイギリス版（GAMESS-UK）に枝分かれして、1997年にアメリカ版を元にして ロシアで Firefly（枝分かれしたときの名前は PC-GAMESS）の開発がはじまりました。

この３つの異なるバージョンの GAMESS は、別々のグループで独立して開発されています。より効率的に計算できるように改良されたり、新しい機能が加えられてきたので、現在では、お互いに全く異なる性質のものになっています。

アメリカ版 GAMESS

GAMESS-US は、アイオワ州立大学（アメリカ）の Mark Gordon 教授 の研究室が中心になって開発されています。学術用途のみならず、商用に関しても無償利用できるという点が魅力です。

GAMESS-US は無償で入手できるのですが、オープンソースではありません。使用するときには、プログラムの再配布やソースコードの再利用を禁止するライセンス条項を遵守する必要があります。

また、GAMESS-US を利用した研究成果を公表する場合には、開発者らによる下記の原著論文を引用する必要があります。

G. M. J. Barca, et al., J. Chem. Phys., Vol. 152, 154102 (2020)

イギリス版 GAMESS

GAMESS-UK は、Computing For Science（CFS）社とダレスベリー研究所（イギリス）で開発されています。イギリス国内での学術用途に対しては無償で配布されていますが、イギリス国外や商用での用途に対しては有償での配布となっています。興味はあるのですが、山本はまだ使ったことはありません。

Firefly

Firefly は、モスクワ大学（ロシア）で開発、無償で配布されています。

1997年頃から GAMESS-US のソースコードを元にして開発が始まり、Intel 社製 CPU などで効率的に動作するように最適化されています。GAMESS-US から枝分かれしたときには PC-GAMESS という名前だったのですが、Firefly という名前に変わりました。

公開されているベンチマークの結果 をみると、密度汎関数法という方法を用いて量子化学計算をおこなった場合には、GAMESS-US よりも計算にかかる時間が短くて、商用パッケージである Q-Chem というソフトウェアに並ぶくらいの計算スピードになっているようです。

この講座では

この講座では、量子化学計算プログラムの代表的な無償パッケージである GAMESS-US を紹介します。便宜のために、以降では GAMESS-US を GAMESS と表記することにします。

電子相関を扱う計算方法

動的電子相関とは？

Hartree-Fock 法は、電子相関という、電子同士の相互作用（短距離での電子間衝突・反発など）を平均化して扱うという近似をしているため、定量的精度については注意をする必要があります。このような電子同士の相互作用は、あとで登場する静的電子相関と区別するために、動的電子相関と呼ばれることもあります。

たとえば、水分子１個の場合でも、Hartree-Fock 法で考慮できない電子相関エネルギーは 140 kcal mol−1 程度にもなります。

動的電子相関を扱う計算方法

GAMESS は、平均場近似である Hartree-Fock 法 をはじめとして、量子化学計算の様々な手法を実行できます。GAMESS の大きな特徴は、量子化学計算の高度な機能（電子相関補正や励起状態計算など）について、メジャーのものからマイナーなものまで、豊富に揃っていることです。

GAMESS では動的電子相関による効果を補正する方法として、Møller-Plesset 摂動法、配置間相互作用（CI：Configuration Interaction）法、結合クラスター法という、高精度な計算を実行できます。

二次の Møller-Plesset (MP2：second-order Møller-Plesset) 摂動法は、計算コストを比較的抑えながら電子相関の効果を大雑把ながらも比較的精度良く見積もることができるため、生体分子など、大規模な分子系に対する電子相関補正として用いられることが多いように思います。

化学反応にともなうエネルギー変化に基づいて反応速度を議論したい場合など、高い定量性が求められる応用研究に多く利用されてるのは、結合クラスター法を用いた CCSD(T) レベルだと言われています。

先述した水分子の場合、電子相関に由来する誤差は、MP2 摂動法では 8 kcal mol−1 程度、CCSD(T) レベルでは 1 kcal mol−1 以下になり、Hartree-Fock 法に比べると、定量的精度について大幅に改善することができます。

ただし、計算手法が高度になるほど、計算するためのコスト（計算に必要な時間やコンピュータの性能）も大きくなってしまうことがほとんどなので、目的に見合った精度とコストのバランスを考えることも大事になります。

静的電子相関とは？

化学反応が起こる様子を追跡しようとすると、化学結合の解離や生成が起こるような領域では、複数の電子配置がエネルギー的に近接する場合があって、量子力学的共鳴に由来する電子間相互作用が顕著となります。このような相互作用のことを静的電子相関と呼びます。

典型例な静的電子相関の効果は、たとえば、水素分子のラジカル開裂にも現れます。

水素分子について、水素原子同士の結合を切断するために必要となるエネルギー（結合エネルギーと呼びます）は、正確に解析してみると 4.75 eV になります。

しかし、Hartree-Fock 法を用いて結合エネルギーを解析してみると、その値は 3.64 eV となり、正確な値とは大きく異なってしまいます。このように定量性を欠いた結果となってしまうのは、水素分子の解離に伴って、この分子の基底電子状態と励起電子状態がエネルギー的に近くなり、２つの状態間の静的電子相関が顕著になったからです。

静的電子相関を扱う計算方法

これまでに登場した計算方法は、電子状態を１つの電子配置のみで記述する近似法でした。静的電子相関について、そのふるまいを正しく考慮するためには、電子状態を複数の電子配置で記述する多配置SCF（MCSCF：Multi Configurational SCF）法と呼ばれる方法が必要となります。

GAMESS では、最も一般的な MCSCF 法である完全活性空間 SCF（CASSCF：Complete Active Space SCF）法をはじめとして、静的電子相関の寄与を考慮するためのさまざまな計算方法を使うことができます。

たとえば 多参照 SCF（MRSCF：Multi Reference SCF）法は、MCSCF 法で求めた波動関数に対して動的電子相関を考慮する方法です。GAMESS では、摂動論に基づくMRMP（Multi Reference Møller-Plesset）法などを利用することで、金属錯体の励起状態など、静的・動的電子相関が絡む複雑な電子状態に関しても定量的精度で各種物性を求めることができます。

密度汎関数法

密度汎関数法とは？

密度汎関数法（DFT：Density Functional Theory） は、近年、研究開発の最前線で大活躍している計算手法です。あとで説明するように、DFT は（動的）電子相関の寄与について、 Hartree-Fock 法とほぼ同程度の計算コストで考慮することができるからです。

DFT は、少し専門的な言い方をすると、電子密度を試行関数とする多電子状態問題の近似解法だと説明することができます。つまり、これまでに紹介してきた Hartree-Fock 法など、波動関数を試行関数とする方法とは、その基盤となる考え方が大きく異なっています。DFT に興味が湧いたひとには、次の優れた教科書をオススメします。

  • 常田 貴夫（著）密度汎関数法の基礎 (2012)。密度汎関数法について、理論的な基礎から様々な汎関数の種類まで、この分野で活躍する第一線の研究者によって、その魅力が熱く語られています。書籍版（6,050円）と Kindle 版（4,840円）。
密度汎関数法の基礎 (KS物理専門書)
講談社
¥6,050 （2024/04/13 22:03時点 | Amazon調べ）
Amazon

GAMESS は、DFT に基づく電子状態計算の機能も豊富です。DFT の計算精度と信頼性は、電子密度と系のエネルギーを関係付ける（密度）汎関数の種類に依存します。GAMESS には、一般化密度勾配近似（GGA：Generalized Gradient Approximation）に基づく各種の汎関数が実装されています。

たとえば、基本的な BLYP （Becke-Lee-Yang-Parr）汎関数・PBE（Perdew-Burke-Ernzerhof）汎関数、Hartree-Fock 交換項と組み合わせた混成 GGA 型の B3LYP 汎関数・PBE0 汎関数など、さまざまな種類の汎関数を利用することができます。

密度汎関数法が得意なこと・苦手なこと

DFT は、電子間相互作用を含む汎関数を導入することで、Hartree-Fock 方程式とほぼ同様なKohn-Sham 方程式を解くだけで、（動的）電子相関の寄与を考慮することが可能となります。したがって、利用する汎関数が適切であれば、Hartree-Fock 法を使うくらいの安価な計算コストで、MP2 摂動法レベルの電子相関効果を含む精度の解析結果を得ることができます。

このような魅力から DFT は、Hartree-Fock 法が苦手とする金属含有系をはじめとして、幅広い物質群の応用計算に利用されています。

一方で DFT の弱点として、長距離電子相関の見積もりを不得意にしています。このため、分子同士に働く相互作用のうち、ファンデルワールス（van der Waals）相互作用を過小評価してしまい、分子集合体系の安定性などを正しく評価できないことが課題として挙げられていました。GAMESS では、長距離領域での電子間相互作用を補正する LC（Long-range Correction）法を実装するなど、DFT をより幅広く活用するためのさまざまな改良が続けられています。

巨大分子系を扱う計算方法

GAMESS には、分子集合体や生体分子などの巨大分子系を効率的に解析する計算方法も実装されています。

現在のバージョンでは、巨大分子系を扱おうとするときの助けになるものとして、たとえば、フラグメント分子軌道（FMO：Fragment Molecular Orbital）法、分割統治（DC：Divide and Conquer）法、Elongation 法 など、さまざまな計算方法を利用することができます。

この中で FMO 法は、その名称の通りに、巨大分子系をフラグメントに分割することで、大規模となってしまう電子状態を効率的に解くことができる計算方法です。

例えば、創薬では薬物・受容体間の定量的な相互作用解析が分子設計の基軸的な指標となります。FMO 法は、タンパク質複合体の相互作用エネルギーに関しても、Hartree-Fock 法や MP2 摂動法の計算精度で解析可能です。したがって FMO 法は、創薬・生物工学をはじめとして、幅広い応用分野への展開が期待されています。

利用可能な基底関数

基底関数とは？

基底関数は、電子波動関数を数値的に記述するための基盤となるものです。どのような分子を解析したいのか、何を調べたいと思っているのか、どのような計算方法を用いるのか、それぞれに応じて、適切に選択する必要があります。

量子化学計算プログラムの多くは、基底関数として各原子に中心を置くGauss 型関数を使っています。GAMESSには、Huzinaga と Dunning によって開発された DZV（double zeta valence）基底関数、Pople らによって開発された 6-31G 基底関数など、基本的なGauss 型基底関数系が組み込まれています。

分極関数と分散関数

分子の複雑な構造を適切に記述したい場合には、各原子上に配置した基底関数に 分極関数（polarization function） を追加することで、電子分布が柔軟に変形する自由度を与えることができます。Pople らの基底関数の場合、基盤となる 6-31G に分極関数を加えた基底関数（6-31G(d,p) あるいは 6-31G** と表記）が常用されています。

また、負電荷を帯びた分子は、中性分子と比較して、電子分布が広がっている場合があります。このような場合、物性諸量を正しく見積もるためには、電子分布の広がりを記述するために 分散関数（diffuse function） を加えた基底関数を用いることができます。

GAMESS は、分極関数や分散関数などのような補助関数の追加も簡単で、計算対象に適切な基底関数系を柔軟に準備することができます。

高精度計算に適した基底関数

これまでに登場した DZV 基底関数や 6-31G 基底関数は、平均場描像に基づく Hartree-Fock 法、電子相関をあらわに扱う必要のない DFT などに有用な基底関数系です。

一方、電子相関の寄与をあらわに扱う MP2 摂動法や結合クラスター法などで信頼性の高い結果を得るには、基底関数の選び方に注意が必要となる場合があります。

GAMESS では、電子相関を取り込んだ高精度計算に適した基底関数として Dunning らの cc-pVnZ 基底関数（n = D, T, Q, 5, 6）が実装されています。この基底関数系では、cc-pVDZ が応用研究の中で頻繁に用いられるのですが、電子相関効果の取り込みが不十分である場合もあります。10 kcal mol−1 程度のエネルギー差を定量的に議論したいときには、可能であれば cc-pVTZ 程度の基底関数を CCSD(T) レベルの計算手法と組み合わせて用いる必要があるように思います。

周期性を持つ分子系は？

固体表面や結晶などの周期性を持つ分子系に興味がある場合には、原子を展開中心とする Gauss 型基底を用いてその電子状態を解析しようとすると、難しさを伴うことが多いです。したがって、一般的には、GAMESS が得意な解析可能な対象は主として孤立分子系に限られる と言えます。周期性を持つ分子系に対しては、平面波を基底関数とする計算化学プログラム（たとえば VASP など）の方が助けになるかと思います。

解析可能な各種物性

多くの量子化学計算プログラムは、系のエネルギーだけではなく、原子核に対するエネルギー勾配や二次微分を解析的に求めることができます。

GAMESS は、エネルギー勾配や二次微分に基づいて、分子の平衡構造や振動状態など、材料開発などの基盤となるさまざまな物性情報を理論的に導くことができます。

分子の立体構造

GAMESS では、各原子核に働く力（エネルギー勾配）の方向にカタチをちょっとずつ変化させて、分子がより安定となるように（エネルギーが小さくなるように）動かすことで、平衡状態にある分子の立体構造を半自動的に最適化（エネルギー最小化）することができます。

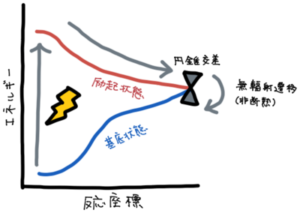
また、ある化学反応について、遷移状態理論に基づいて反応が進行する速度などを議論しようとするときには、その反応に伴う遷移状態を詳しく調べる必要があります。遷移状態は、ポテンシャルエネルギー曲面上の鞍点にあるので、探索方法にも少し工夫が必要です。GAMESS には、遷移状態にある分子の立体構造についても、効率的に探索する機能が備わっています。

さらに GAMESS では、平衡構造と遷移状態を繋ぐ固有反応座標（IRC：Intrinsic Reaction Coordinate）を解析することも可能であり、化学反応の分子機構をエネルギー変化の観点から詳細に調べることもできます。

分子の振動状態

GAMESSはエネルギーの 二次微分（力の定数） を用いて分子の振動状態も解析できます。

振動解析は、赤外・ラマンスペクトルを読み解く際、振動バンドの解釈を補助する便利な手段として広く利用されています。

しかし、実際に観測された赤外・ラマンスペクトルと計算で得られた振動解析の結果を比較したときに、両者が著しく異なる場合も多々あります。標準的な振動解析は、分子運動を調和振動子的にふるまうものと仮定して扱うのですが、実際の分子振動は調和近似から逸脱した非調和的なふるまいを示すためです。

GAMESS には非調和性を考慮した振動状態を解析できる VSCF（Vibrational SCF）法も実装されており、水素結合錯体などの非調和性が顕著に現れる系に対しても信頼性の高い振動解析ができます。

分子の振動解析に関して、こちらの記事で、分子科学若手の会・夏の学校で用いた「振動解析再入門：振動計算の基礎とスペクトル解釈への応用」というノート（PDFファイル）を公開しています。

GAMESS をインストールしよう

GAMESS の入手

GAMESS プログラムは、公式サイトから無償で入手できます。サイト内の「GAMESS Registration System」にメールアドレスを登録すると、ダウンロード用の URL アドレスが記載された電子メールが届きます。この電子メールには、ダウンロードに必要なユーザ名と、一時アクセス用のパスワードも記載されています。

ダウンロードの際、GAMESS プログラムのファイル形式として、コンパイル済みの実行形式とソースコードの２種類を選ぶことができます。

コンパイル済の実行形式

現時点では、コンパイル済みの実行形式として Windows 環境用と Mac OS X 環境用を選択できるはずです。山本は、ノートパソコンの環境（Apple Mac OS X; Intel 64-bit x86系プロセッサ）に合わせて、最新版（Version 2020 R.1）の Mac OS X 用パッケージを入手しました。

パッケージには、コンパイル済みのプログラム（gamess.30Jun2020R1.x と ddikick.x）、実行用のシェルスクリプト（gms と rungms）などが含まれます。これらのファイルを適当な場所に移動して、実行用のスクリプトを用いて GAMESS プログラムを起動することで、面倒なコンパイル作業抜きで量子化学計算を手軽に実行できます。

ソースコードからコンパイル

Unix や Linux 環境では、ソースコードを入手してコンパイルする必要があります。コンパイル手順の詳細は gamess ディレクトリ内の README.md などに記載されています。コンパイルの手順は GAMESS のバージョンや計算機環境に依存して異なりますが、ここでは山本が さくらのVPS（Intel x86_64系プロセッサ; CentOS 7）で最新版（Version 2021 R.2）の GAMESS ソースコードをコンパイルした手順を示してみます。

tar xvfz gamess-current.tar.gz -C /usr/local
cd /usr/local/gamess
./config
make ddi
make modules
make -j 2 >& make.log &

基本的には、ダウンロードした圧縮ファイル（gamess-curent.tar.gz）を展開した後、設定用のスクリプト config を実行することで、コンパイルに必要な情報を（install.info）に書き出し、make を順次実行します。以上の手続きを経て無事にコンパイルが完了すると、実行形式のファイルとして、gamess.00.x と ddi/ddikick.x ができます。

GAMESS の入力ファイル

GAMESSの基本的な実行手順では、テキストエディタなどを使って入力ファイルを作成した後、実行用のシェルスクリプト（rungms）を使ってプログラム本体（ddikick.x と gamess.00.x）を起動することで量子化学計算を実行します。

GAMESS で実行する計算方法や分子座標などの設定情報は、入力ファイルで指定します。具体例として、Hartree-Fock 法と 6-31G 基底関数を用いて水分子（H2O）のエネルギー計算を行う場合の入力例を示します。

 $CONTRL
   RUNTYP=ENERGY
   SCFTYP=RHF
 $END
 $BASIS
   GBASIS=N31 NGAUSS=6
 $END
 $DATA
Water (H2O) HF/6-31G Energy
Cnv 2

O 8.0 0.0000000000 0.0000000000 -0.0379028450
H 1.0 0.7851705218 0.0000000000  0.4962402356
 $END

上記のように、入力ファイルは幾つかの設定グループで構成されます。各設定グループは $GROUP で始まり $END で終わるという基本構造を持ちます。この $GROUP には、$CONTRL や $BASIS など、設定グループ毎に固有の名称が入ります。

注意点として、$ 記号の直前には１個分の空白が必要です。忘れないようにしましょう。また、入力情報として読み込まれる各行の長さは80文字以内に制約されます。

上記の例は大文字で入力していますが、小文字でも大丈夫です。設定グループ内の入力規則としては、$CONTRL と $BASIS のような KEYWORD=OPTION 形式と、$DATA のような行型のデータ構造を持つ形式があります。

基本的な次の設定グループについて、いくつか説明してみましょう。

CONTRL 設定グループ

$CONTRL は、主に計算方法を指定する設定グループです。

SCFTYP キーワードでは、波動関数の計算方法を指定します。指定できるオプションとしては、制限 HF（RHF：Restricted HF）法、非制限 HF（UHF：Unrestricted HF）法、MCSCF 法などがあります。水分子は全ての電子が対を形成した閉殻系なので、計算には RHF 法を用います。

RUNTYP キーワードでは、計算内容を指定します。指定できるオプションとしては、エネルギー計算（RUNTYP=ENERGY）の他に、構造最適化（RUNTYP=OPTIMIZE）や振動解析（RUNTYP=HESSIAN）などがあります。

BASIS 設定グループ

$BASIS では、基底関数に関する設定をおこないます。

GBASIS キーワードで指定できる基底関数の種類としては、Pople らが開発した 6-31G 基底関数（GBASIS=N31 NGAUSS=6）の他に、Huzinag と Dunning が開発した DZV 基底関数（GBASIS=DZV）、Dunning の cc-pVDZ 基底関数（GBASIS=CCD）などがあります。

DATA 設定グループ

$DATA は、分子座標を指定する設定グループであり、行型のデータ構造を持っています。

１行目では、任意のタイトルを指定します。タイトルは出力ファイルにも反映されるので、分子の名称や計算方法などを記入しておくと、計算した後の整理に役立つかと思います。

２行目では、分子の対称性を指定します。水分子は２本の等しい OH 結合を持つ二等辺三角形型であり、C2​ 回転軸とσv ​鏡映面を対称要素に持つ C2v ​対称群に属しています。分子の幾何構造をC2v ​対称群に指定する場合、GAMESSでは Cnv 2 と入力します。

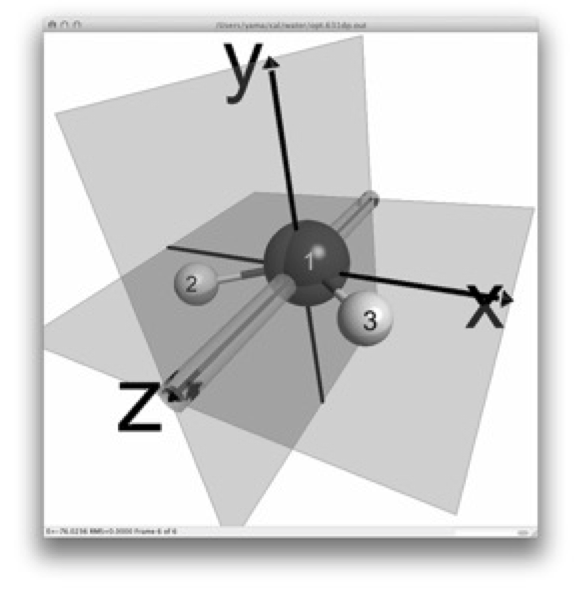
上の図は、分子の立体構造と対称要素（回転軸と鏡映面）を示しています。この図の描画には、MacMolPlt を用いました。MacMolPlt は、GAMESS の入力ファイルの作成支援や分子軌道の可視化などの機能を備えた高機能な分子ビュアーであり、 で無償配布されています。

３行目に空行を挟み（２行目で C1 ​対称性を指定した場合、この空行は必要ありません）、４行目以降で分子座標を指定します。

４行目以降では、原子ラベル、原子番号、xyz 座標の順番で分子座標を入力します。原子ラベルは任意の文字列であり、原子種は原子番号で指定します。つまり、原子ラベルは複数の原子を区別する目的で、Oxygen1 や Oxygen2 のようにも記入することもできます。

GAMESS で xyz 座標を入力する場合、座標軸の選び方に独自のルールがあります。たとえば、今回のような C2v ​対称構造の場合、分子面は xz 平面、分子軸が z 軸となるように座標軸を決める必要があります。このようなルールは指定する対称性ごとに異なるので、入力の際には GAMESS マニュアルを確認する必要があります。なお、ここで入力する xyz 座標は１個の酸素原子と１個の水素原子に対してのみであり、３個目の水素原子は２行目で指定した C2v ​対称性を満たすよう自動的に配置されます。

上記のように分子構造を xyz 座標で指定する場合、GAMESS 独自のルールに慣れるまでは戸惑うことがあるかも。GAMESS では、xyz 座標形式の他に、Z-Matrix 形式で分子構造を指定することも可能であり、Z-Matrix 形式の方が便利な場合が多いように思います。

Z-Matrix 形式は３種類の内部座標（結合長・結合角・二面角）で分子構造を表現する方法であり、化学結合の構造を直感的に把握できるなどの利点があります。水分子の計算について、分子座標を Z-Matrix 形式で記述した入力例を示しておきます。

 $CONTRL
   SCFTYP=RHF
   RUNTYP=ENERGY
   COORD=ZMT
 $END
 $BASIS
   GBASIS=N31 NGAUSS=6
 $END
 $DATA
Water (H2O) HF/6-31G Energy
Cnv 2

O
H  1  1.0
H  1  1.0  2  110.0
$END

Z-Matrix 形式で分子座標を記述する場合、$CONTRL に COORD=ZMT オプションを追加して、$DATA の４行目から入力をはじめます。この入力例の場合、２番目の水素原子は１番目の酸素原子から 1.0 Å の距離に配置されます。３番目の水素原子は、２番目と同様に OH 結合長を 1.0 Å として、HOH 結合角が110.0 度となるように配置されます。最初に紹介した入力例の xyz 座標は、ここで示す Z-Matrix 形式で指定した分子構造に等しく、計算結果も有効桁数の範囲内で一致します。

GAMESS を実行しよう

GAMESS を実行する

GAMESS には、プログラムの実行手続きをまとめたシェルスクリプト（rungms）が付属しています。基本的には、この rungms を介して GAMESS プログラム（ddikick.x と gamess.00.x）を起動することになります。この rungmsスクリプトは 1400 行以上もありますが、GAMESS を実行するには記述内容の一部を各自の計算機環境に応じて編集する必要があります。編集内容は計算機環境に依存するのですが、たとえば、計算の中間ファイルを一時的に保存するディレクトリを初期設定（/scr/$USER）から計算環境に合わせた場所（/work）に変更する場合、該当箇所を次のように編集します。

set SCR=/work

  初期設定では、ホームディレクトリ直下の $HOME/scr に幾つかのテキスト形式のデータ（分子軌道係数を含む PUNCH ファイルなど）が出力されるので、計算実行の前にあらかじめこのディレクトリ（$HOME/scr）を作成しておく必要があります。あるいは次のように、入力ファイルと同じディレクトリにデータファイルを出力するように rungms スクリプトの設定を変更することもできます。

setenv PUNCH ./$JOB.dat

設定後、入力ファイルのあるディレクトリに移動して rungms スクリプトを実行します。入力ファイルの名前が exam.inp の場合、基本的な実行方法は次のようになります。

% rungms exam >& exam.log

最初の引数には入力ファイルの拡張子（.inp）を除いた部分を指定します。計算結果は exam.log に出力されます。計算が終了した後、一部のデータが rungms に設定したディレクトリに出力されるはずです。このディレクトリ内に計算データ（$HOME/scr/exam.datなど）が残っていると rungms スクリプトが強制終了するため、計算終了後にファイル群を移動あるいは消去する必要があります。

GAMESS の出力ファイルを読み取る

GAMESSの計算結果は rungms スクリプトの実行時に指定したファイル（先述の例では exam.log）に出力されます。

今回の場合、PROPERTY VALUES FOR THE RHF SELF-CONSISTENT FIELD WAVEFUNCTION というメッセージ以降に、エネルギー値（ENERGY COMPONENTS）、部分電荷（MULLIKEN AND LOWDIN POPULATION ANALYSES）、結合次数（BOND ORDER AND VALENCE ANALYSIS）、双極子モーメント（ELECTROSTATIC MOMENTS）などの物性情報が出力されます。

エネルギーに関する出力部分を抜き出すと以下のようになり、この場合、水分子の全エネルギーは−75.980769 Hartree（1 Hartree = 27.2114 eV）であることが分かります。

 -----------------
 ENERGY COMPONENTS
 -----------------
                                （省略）
                 TOTAL ENERGY =     -75.9807690629

GAMESS の実践例

量子化学の計算手法は、多電子状態問題の近似解法であり、近似精度によっては必ずしも物理化学的に正しい結果が得られるという保証はありません。可能な場合には、実験結果と比較検討しながら計算経験を積むことで、各種手法の適用範囲に関する実際的感覚を身に付ける必要があるように思います。

ここでは、量子化学計算で頻繁に実行される構造最適化と振動解析の具体例を通して、GAMESS の計算結果から物性諸量を正しく読み解くための実践例を紹介してみます。

構造最適化

構造最適化は、入力した分子座標を出発点として、系のエネルギーが安定化する方向に少しずつ変化させることで分子の安定構造を探索する方法です。はじめに、水分子を対象として、HF法と6-31G基底関数を用いた構造最適化の計算例を示します。

 $CONTRL
   SCFTYP=RHF
   RUNTYP=OPTIMIZE
   COORD=ZMT
 $END
 $BASIS
   GBASIS=N31 NGAUSS=6
 $END
 $DATA
Water (H2O) HF/6-31G Geometry Optimization
Cnv  2

O
H   1   1.0
H   1   1.0   2   110.0
$END

構造最適化は $CONTRL に RUNTYP=OPTIMIZE を指示することで実行されます。計算が終了した後、出力ファイルに「EQUILIBRIUM GEOMETRY LOCATED」のメッセージがあれば、構造探索が無事収束して安定構造に辿り着いています。分子座標を Z-Matrix 形式で指定した場合、次のように、安定構造は xyz 座標と共に Z-Matrix 形式でもファイルに出力されます。

THE CURRENT FULLY SUBSTITUTED Z-MATRIX IS
 O
 H      1   0.9496323
 H      1   0.9496323  2   111.5459321

この出力結果から、HF/6-31G レベルで構造最適化した場合、安定構造の OH 結合長は 0.9496 Å、HOH 結合角は 111.55 度であることが分かります。一方、実験的に決定された水分子の幾何構造については、次のことが知られています。

OH 結合長HOH 結合角
0.9575 Å104.51 度

構造最適化が無事収束しているにも係わらず、実験値と比較すると、HOH 結合角は 7% 程度の比較的大きな誤差を含んでいます。このような誤差の原因として、今回の計算に用いた基底関数が適切ではなく、化学結合の構造を正しく記述するには分極関数を加える必要があるのかもと推測されます。

そこで次に、基底関数の精度を改善した計算に挑戦してみましょう。再計算の入力例を示します。

 $CONTRL
   SCFTYP=RHF
   RUNTYP=OPTIMIZE
   COORD=ZMT
 $END
 $BASIS
   GBASIS=N31 NGAUSS=6 NDFUNC=1 NPFUNC=1
 $END
 $DATA
Water (H2O) HF/6-31G(d,p) Geometry Optimization
Cnv  2

O
H  1  0.9496323
H  1  0.9496323  2  111.5459321
 $END

基底関数の変更は $BASIS にオプションを追加することでおこないます。ここでは分極関数として、各原子の価電子軌道より１つだけ方位量子数の大きな形状を持つ補助関数を加えました。具体的には、酸素原子にd軌道型関数（NDFUNC=1）、水素原子にp軌道型関数（NPFUNC=1）を追加しています。また、$DATAでは、前回のHF/6-31Gレベルの計算で得た結果を初期構造に用いています。

再計算後、安定構造は Z-Matrix 形式では次のように出力されます。

THE CURRENT FULLY SUBSTITUTED Z-MATRIX IS
 O
 H      1   0.9430602
 H      1   0.9430602  2   105.9649900

HF/6-31G(d,p) レベルで構造最適化した場合、HOH 結合角は 105.96 度となり、安定構造の計算精度が改善されたことが分かります。

以上のように、対象とする分子の特徴を定量的精度で正しく記述するには、計算に用いる基底関数を適切に選択する必要があります。

振動解析

振動解析は分子固有の振動数と赤外強度を理論的に計算する方法であり、実験的に測定された赤外スペクトルの解釈を補助する手段として活用されています。

はじめに、調和近似（分子運動が調和振動子的にふるまうと仮定する近似）に基づく振動解析の計算例を示します。

 $CONTRL
   SCFTYP=RHF
   RUNTYP=HESSIAN
   COORD=ZMT
 $END
 $BASIS
   GBASIS=N31 NGAUSS=6 NDFUNC=1 NPFUNC=1
 $END
 $DATA
Water (H2O) HF/6-31G(d,p) Normal Frequency Analysis
Cnv  2

O
H  1  0.9430602
H  1  0.9430602  2  105.9649900
 $END

調和振動解析は $CONTRL に RUNTYP=HESSIAN を指示することで実行されます。キーワードであるHESSIAN の名称は、振動解析にエネルギーの二次微分行列（Hessian行列）を用いることに由来します。注意点として、振動解析を実行する場合、$DATA には同じ計算レベルで最適化した安定構造を分子座標として用いる必要があります。

計算が終了した後の出力ファイルには、「NORMAL COORDINATE ANALYSIS IN THE HARMONIC APPROXIMATION」のメッセージ以降に、振動数と赤外強度が次のように出力されます。

                  6           7           8           9
   FREQUENCY:    14.57     1769.68     4147.54     4264.52
    SYMMETRY:     B2          A1          A1          B1
REDUCED MASS:  1.10528     1.08308     1.04479     1.08331
IR INTENSITY:  7.98655     2.47512     0.38561     1.36962

水分子の場合、合計９個のモードが出力されます。このうち最初の６個は分子の並進運動・回転運動モードであり、７番目以降の３個のモードが変角振動（７番目）・対称伸縮振動（８番目）・逆対称伸縮振動（９番目）に対応します。

さて、実験的に観測される水分子の振動数は、それぞれ、次のようになることが知られています。

変角振動対称伸縮振動逆対称伸縮振動
1595 cm−13657 cm−13756 cm−1

したがって HF/6-31G(d,p) レベルの計算結果は、安定構造は実験値と比較的良く一致するにも係わらず、振動数に関する誤差は最大 14% 程度と大きいことが分かります。このように著しい誤差が生じる原因としては、電子相関の寄与と非調和性の寄与が考えられます。

そこで次に、計算精度を改善するための方策として、MP2 摂動法を用いて電子相関の寄与を考慮した振動解析に取り組んでみましょう。

 $CONTRL
   SCFTYP=RHF
   MPLEVL=2
   RUNTYP=HESSIAN
   ISPHER=1
   COORD=ZMT
 $END
 $BASIS
   GBASIS=CCT
 $END
 $DATA
Water (H2O) MP2/cc-pVTZ Normal Frequency Analysis
Cnv 2

O
H  1  0.9590752
H  1  0.9590752  2  103.5180597
 $END

MP2摂動法を実行する場合、$CONTRL で MPLEVEL=2 を設定します。先述したように、電子相関の寄与を適切に考慮するには基底関数の選び方にも注意が必要です。今回は Dunning の cc-pVTZ 基底関数を用いました。基底関数に cc-pVTZ を用いる場合、$BASIS のキーワードを GBASIS=CCT に変更するのに加えて、$CONTRL に ISPHER=1 を追加する必要があります。$DATA には振動解析と同じ計算レベル（MP2/cc-pVTZ）で構造最適化した内部座標（OH結合長：0.9591 Å；HOH結合角：103.52 度）を入力しています。

この場合、振動数の計算結果は次のように出力されました。

                  6           7           8           9
   FREQUENCY:    17.05     1651.86     3855.49     3975.79
    SYMMETRY:  CV B2          A1          A1          B1
REDUCED MASS:  1.12575     1.08260     1.04524     1.08088
IR INTENSITY:  5.93899     1.52669     0.13572     1.30620

MP2摂動法を用いることで、各モードの振動数は低波数方向へシフトすることで実験値に近づくことが分かります。しかし、電子相関補正を利用しても、振動数の計算結果には 6% 程度の誤差が依然として残っています。

分子振動をより定量的精度で解析したい場合には、調和近似を越えた取り扱いが必要となります。GAMESS では、非調和性を考慮した振動解析として、VSCF法を利用することができます。そこで最後に、GAMESS による非調和振動解析にも取り組んでみましょう。

 $CONTRL
   SCFTYP=RHF
   MPLEVL=2
   RUNTYP=VSCF
   ISPHER=1
   COORD=ZMT
 $END
 $BASIS
   GBASIS=CCT
 $END
 $DATA
Water (H2O) MP2/cc-pVTZ Vibrational SCF Calculation
Cnv 2

O
H  1  0.9590752
H  1  0.9590752  2  103.5180597
 $END
 $HESS
（省略） ← PUNCHファイルの出力
 $END

VSCF 法は $CONTRL で RUNTYP=VSCF を指示することで実行できます。VSCF 法では、計算に Hessian 行列を用いるため、調和振動解析（RUNTYP=HESSIAN）後に出力される PUNCH ファイル（rungms スクリプトの初期設定では $HOME/scr に出力される）の $HESS 出力グループを上記入力例のように貼り付ける必要があります。

計算が終了した後、非調和補正を行った振動数は次のように出力されました。

RESULTS OF VIBRATIONAL SCF CALCULATION: (FREQUENCIES IN CM-1)
MODE  HARMONIC   DIAGONAL     VSCF      PT2-VSCF
  9    3975.79    4068.90    3801.91    3764.94
  8    3855.49    3774.06    3742.53    3682.29
  7    1651.86    1638.31    1591.52    1586.01

得られた非調和振動解析の結果は、実験値と非常に良く一致することが分かります。ただし、VSCF 法の計算負荷は大きく、調和近似に比べて数倍程度の計算時間が必要になるかも知れません。

分子振動の非調和性については、こちらの記事で紹介する「振動解析再入門：振動計算の基礎とスペクトル解釈への応用」というノート（PDFファイル）で、詳しく紹介しています。

おわりに

このノートでは、無償で利用できる本格的な量子化学計算プログラム GAMESS の基本的な使い方について、ざっくりとご紹介してみました。このノートが、量子化学計算に興味を持つひとの一助となって、研究開発などで GAMMESS を使ってみようと思う契機となれば幸いです。

このノートについて、もし何かお気付きのことがあり、それを山本に伝えておきたいと思われた方は、質問・感想・コメントをお送りください。

lect
よかったらシェアしてね！
  • URLをコピーしました！

この記事を書いた人

山本 典史のアバター 山本 典史

千葉工業大学 応用化学科 教授。専門はコンピュータ化学、コンピュータを使って分子を解析しています。化学の学びを身近にすることにも興味を持っています。

関連記事

目次